Lessico
Claudio Tolomeo
incisione di Theodor de Bry
(1528-1598)
da Bibliotheca chalcographica di Jean-Jacques Boissard - 1669
Astronomo, matematico e geografo greco (100 - 178 ca. dC). Ultimo rappresentante dell'astronomia greca, secondo la tradizione svolse la sua attività d'osservatore nel tempio serapeo di Canopo, vicino ad Alessandria d'Egitto. Elaborò la più compiuta sintesi astronomica dell'antichità che trattò nell'opera Megálë mathëmatikë sýntaxis (Grande sintassi matematica), rimasta celebre con l'appellativo Megístë sýntaxis (Grandissima sintassi) che tradotto in arabo al-Magisti ha dato luogo al termine “almagesto”.
Utilizzando
i dati raccolti dai suoi predecessori, in particolare da Ipparco, Tolomeo
costruì un sistema del mondo che,
pur ammettendo a priori l'immobilità della Terra, riusciva, grazie a
espedienti di estrema complessità, a rappresentare con soddisfacente
precisione le traiettorie apparenti del Sole![]() , della Luna
, della Luna![]() e dei cinque pianeti
allora conosciuti.
e dei cinque pianeti
allora conosciuti.
Il sistema geocentrico di Tolomeo, che dava solo un'interpretazione cinematica dei moti planetari, fu mantenuto quale unico modello del mondo fino al primo Rinascimento nonostante che nel tardo Medioevo la maggiore precisione delle osservazioni comportasse l'introduzione di decine di nuovi epicicli rendendolo complicato e farraginoso.
Anche come geografo Tolomeo esercitò una notevole influenza sui secoli successivi fino alle grandi scoperte geografiche. Nella Geografia, opera realizzata a completamento del lavoro iniziato da Marino di Tiro, formulò con cura le regole per costruire globi terrestri e carte terrestri piane per mezzo di diversi sistemi di proiezione e raccolse un lungo elenco di posizioni geografiche delle più importanti città e punti costieri. La precisione del reticolo di meridiani e paralleli costruito da Tolomeo era compatibile con le misure di latitudine e longitudine allora dedotte per lo più da rilievi itinerari riportati dai viaggiatori; inoltre Tolomeo adottò per la circonferenza terrestre la valutazione data da Posidonio, inferiore al valore reale di ca. 1/6, per cui tutte le indicazioni di distanza risultavano errate della stessa misura.
Tra le altre opere figurano il trattato di astrologia Tetrábiblos, la cui attribuzione non è del tutto sicura, l'Ottica in cinque libri, di cui il primo è perduto, le Armoniche che contengono la teoria dei suoni usati nella musica greca.


Dal frontespizio di un'edizione della Geografia stampata a Ulm nel 1482

Tolomeo con il quadrante in una stampa antica

Tolomeo mentre osserva il cielo utilizzando un
piccolo quadrante
Firenze - formella del campanile di Giotto
(Colle di Vespignano ca. 1265 - Firenze 1337)

Born
after 83 CE - Roman Province of Egypt
Died 161 CE - Roman Province of Egypt
Occupation: mathematician, geographer, astronomer, astrologer.
Claudius Ptolemaeus (after 83 – 161 CE), known in English as Ptolemy, was a Greek mathematician, geographer, astronomer, and astrologer. He lived in Roman Egypt, and was probably born there in a town in the Thebaid called Ptolemais Hermiou; he died in Alexandria in 161 CE.
Ptolemy was the author of several scientific treatises, three of which would be of continuing importance to later Islamic and European science. The first is the astronomical treatise is now known as the Almagest (Megístë sýntaxis "The Great Treatise", originally Megálë mathëmatikë sýntaxis "Great Mathematical Treatise"). The second is the Geography, which is a thorough discussion of the geographic knowledge of the Greco-Roman world. The third is the astrological treatise known as the Tetrabiblos ("Four books") in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day.
The name
Beyond his being considered a member of Alexandria's Greek society, few details of Ptolemy's life are known. Some scholars have assumed that Ptolemy may have been a Greek, and others, a Hellenized Egyptian. He was often known in later Arabic sources as "the Upper Egyptian", suggesting that he may have had origins in southern Egypt. Ptolemy is also known to have used Babylonian astronomical data.
Ptolemy is a Greek name. It occurs once in Greek mythology, and is of Homeric form. It was quite common among the Macedonian upper class at the time of Alexander the Great, and there are several among Alexander's army, one of whom made himself King of Egypt: Ptolemy I Soter; all the Kings after him, until Rome conquered Egypt, were also Ptolemies. There is no evidence on Ptolemy's ancestry, but most scholars consider it unlikely that Ptolemy was related to the royal family.
Claudius is a Roman name; it implies Ptolemy was a Roman citizen. It would have suited custom if the first Ptolemy who became a citizen (whether it was he or an ancestor) took the nomen from a Roman called Claudius, who was in some sense responsible for the citizenship. If, as was not uncommon, this Roman was the Emperor, the citizenship would have been granted between 41 and 68 CE, when the Claudii were Emperors. The astronomer would also have had a praenomen, which remains unknown.
Astronomy
The Almagest is the only surviving comprehensive ancient treatise on astronomy. Babylonian astronomers had developed arithmetical techniques for calculating astronomical phenomena; Greek astronomers such as Hipparchus had produced geometric models for calculating celestial motions; Ptolemy, however, claimed to have derived his geometrical models from selected astronomical observations by his predecessors spanning more than 800 years, though astronomers have for centuries suspected that his models' parameters were adopted independently of observations. Ptolemy presented his astronomical models in convenient tables, which could be used to compute the future or past position of the planets. The Almagest also contains a star catalogue, which is an appropriated version of a catalogue created by Hipparchus. Its list of forty-eight constellations is ancestral to the modern system of constellations, but unlike the modern system they did not cover the whole sky (only the sky Hipparchus could see).
Through the Middle Ages it was spoken of as the authoritative text on astronomy, with its author becoming an almost mythical figure, called Ptolemy, King of Alexandria. The Almagest was preserved, like most of Classical Greek science, in Arabic manuscripts (hence its familiar name). Because of its reputation, it was widely sought and was translated twice into Latin in the 12th century, once in Sicily and again in Spain. Ptolemy's model, like those of his predecessors, was geocentric and was almost universally accepted until an equally systematic presentation of a heliocentric geometrical model by Nicolaus Copernicus.
His Planetary Hypotheses went beyond the mathematical model of the Almagest to present a physical realization of the universe as a set of nested spheres, in which he used the epicycles of his planetary model to compute the dimensions of the universe. He estimated the Sun was at an average distance of 1210 Earth radii while the radius of the sphere of the fixed stars was 20,000 times the radius of the Earth.
Ptolemy presented a useful tool for astronomical calculations in his Handy Tables, which tabulated all the data needed to compute the positions of the Sun, Moon and planets, the rising and setting of the stars, and eclipses of the Sun and Moon. Ptolemy's Handy Tables provided the model for later astronomical tables or zijes. In the Phaseis (Risings of the Fixed Stars) Ptolemy gave a parapegma, a star calendar or almanac based on the appearances and disappearances of stars over the course of the solar year.
His model and computational methods were adopted and modified in the Arabic speaking world and in India, since they were of sufficient accuracy to satisfy the needs of astronomers, astrologers, timekeepers, calendar keepers, and navigators.
Geography
Ptolemy's other main work is his Geographia. This too is a compilation of what was known about the world's geography in the Roman Empire during his time. He relied somewhat on the work of an earlier geographer, Marinos of Tyre, and on gazetteers of the Roman and ancient Persian Empire, but most of his sources beyond the perimeter of the Empire were unreliable.
The first part of the Geographia is a discussion of the data and of the methods he used. As with the model of the solar system in the Almagest, Ptolemy put all this information into a grand scheme. Following Marinos, he assigned coordinates to all the places and geographic features he knew, in a grid that spanned the globe. Latitude was measured from the equator, as it is today, but Ptolemy preferred in book 8 to express it as the length of the longest day rather than degrees of arc (the length of the midsummer day increases from 12h to 24h as you go from the equator to the polar circle). In books 2 through 7, he used degrees and put the meridian of 0 longitude at the most western land he knew, the "Blessed Islands", probably the Cape Verde islands (not the Canary Islands, as long accepted) as suggested by the location of the six dots labelled the "fortunata" islands near the left extreme of the blue sea of Ptolemy's map here reproduced.
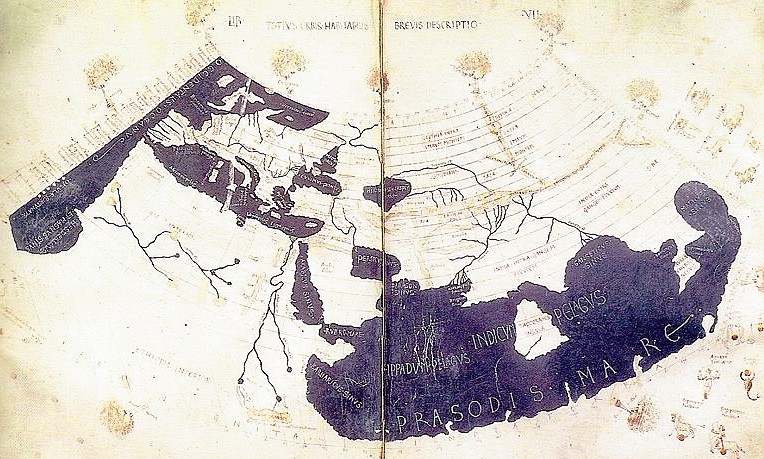
A 15th century manuscript copy of the Ptolemy world map, reconstituted from Ptolemy's Geographia (circa 150), indicating the countries of "Serica" and "Sinae" (China) at the extreme right, beyond the island of "Taprobane" (Sri Lanka, oversized) and the "Aurea Chersonesus" (Malay Peninsula).
Ptolemy also devised and provided instructions on how to create maps both of the whole inhabited world (oikoumenè) and of the Roman provinces. In the second part of the Geographia he provided the necessary topographic lists, and captions for the maps. His oikoumenè spanned 180 degrees of longitude from the Blessed Islands in the Atlantic Ocean to the middle of China, and about 80 degrees of latitude from The Shetlands to anti-Meroe (east coast of Africa); Ptolemy was well aware that he knew about only a quarter of the globe, and an erroneous extension of China southward blocked off any awareness of the Pacific Ocean.
The maps in surviving manuscripts of Ptolemy's Geographia, however, date only from about 1300, after the text was rediscovered by Maximus Planudes. It seems likely that the topographical tables in books 2-7 are cumulative texts - texts which were altered and added to as new knowledge became available in the centuries after Ptolemy (Bagrow 1945). This means that information contained in different parts of the Geography is likely to be of different date.
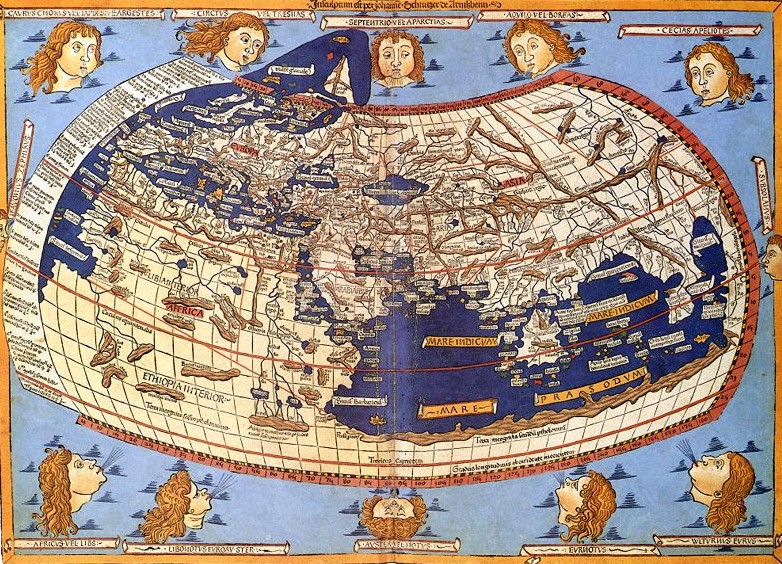
A printed Ptolemaic map from the 15th century
Maps based on scientific principles had been made since the time of Eratosthenes (3rd century BC), but Ptolemy improved projections. It is known that a world map based on the Geographia was on display in Autun, France in late Roman times. In the 15th century Ptolemy's Geographia began to be printed with engraved maps; the earliest printed edition with engraved maps was produced in Bologna in 1477, followed quickly by a Roman edition in 1478 (Campbell, 1987). An edition printed at Ulm in 1482, including woodcut maps, was the first one printed north of the Alps. The maps look distorted as compared to modern maps, because Ptolemy's data were inaccurate. One reason is that Ptolemy estimated the size of the Earth as too small: while Eratosthenes found 700 stadia for a great circle degree on the globe, in the Geographia Ptolemy uses 500 stadia. It is highly probable that these were the same stadion since Ptolemy switched from the former scale to the latter, between the Syntaxis and the Geographia and severely readjusted longitude degrees accordingly. If they both used the Attic stadion of about 185 meters, then the older estimate is 1/6 too large, and Ptolemy's value is 1/6 too small, a difference recently explained as due to ancient scientists' use of simple methods of measuring the earth, which were corrupted either high or low by a factor of 5/6, due to air's bending of horizontal light rays by 1/6 of the earth's curvature. See also Ancient Greek units of measurement and History of geodesy.
Because Ptolemy derived many of his key latitudes from crude longest day values, his latitudes are erroneous on average by roughly a degree (2 degrees for Byzantium, 4 degrees for Carthage), though capable ancient astronomers knew their latitudes to more like a minute. (Ptolemy's own latitude was in error by 14'.) He agreed (Geographia 1.4) that longitude was best determined by simultaneous observation of lunar eclipses, yet he was so out of touch with the scientists of his day that he knew of no such data more recent than 500 years ago (Arbela eclipse). When switching from 700 stadia per degree to 500, he (or Marinos) expanded longitude differences between cities accordingly (a point 1st realized by P.Gosselin in 1790), resulting in serious over-stretching of the earth's east-west scale in degrees, though not distance. Achieving highly precise longitude remained a problem in geography until the invention of the marine chronometer at the end of the 18th century. It must be added that his original topographic list cannot be reconstructed: the long tables with numbers were transmitted to posterity through copies containing many scribal errors, and people have always been adding or improving the topographic data: this is a testimony to the persistent popularity of this influential work in the history of cartography.
Astrology
Ptolemy's treatise on astrology, the Tetrabiblos, was the most popular astrological work of antiquity and also enjoyed great influence in the Islamic world and the medieval Latin West. The Tetrabiblos is an extensive and continually reprinted treatise on the ancient principles of horoscopic astrology in four books (Greek tetra means "four", biblos is "book"). That it did not quite attain the unrivalled status of the Almagest was perhaps because it did not cover some popular areas of the subject, particularly electional astrology (interpreting astrological charts for a particular moment to determine the outcome of a course of action to be initiated at that time), and medical astrology.
The great popularity that the Tetrabiblos did possess might be attributed to its nature as an exposition of the art of astrology and as a compendium of astrological lore, rather than as a manual. It speaks in general terms, avoiding illustrations and details of practice. Ptolemy was concerned to defend astrology by defining its limits, compiling astronomical data that he believed was reliable and dismissing practices (such as considering the numerological significance of names) that he believed to be without sound basis.
Much of the content of the Tetrabiblos may well have been collected from earlier sources; Ptolemy's achievement was to order his material in a systematic way, showing how the subject could, in his view, be rationalized. It is, indeed, presented as the second part of the study of astronomy of which the Almagest was the first, concerned with the influences of the celestial bodies in the sublunar sphere. Thus explanations of a sort are provided for the astrological effects of the planets, based upon their combined effects of heating, cooling, moistening, and drying.
Ptolemy's astrological outlook was quite practical: he thought that astrology was like medicine, that is conjectural, because of the many variable factors to be taken into account: the race, country, and upbringing of a person affects an individual's personality as much if not more than the positions of the Sun, Moon, and planets at the precise moment of their birth, so Ptolemy saw astrology as something to be used in life but in no way relied on entirely.
Music
Ptolemy also wrote an influential work, Harmonics, on music theory and the mathematics of music. After criticizing the approaches of his predecessors, Ptolemy argued for basing musical intervals on mathematical ratios (in contrast to the followers of Aristoxenus and in agreement with the followers of Pythagoras) backed up by empirical observation (in contrast to the overly theoretical approach of the Pythagoreans). Ptolemy wrote about how musical notes could be translated into mathematical equations and vice versa in Harmonics. This is called Pythagorean tuning because it was first discovered by Pythagoras. However, Pythagoras believed that the mathematics of music should be based on the specific ratio of 3:2 whereas Ptolemy merely believed that it should just generally involve tetrachords and octaves. He presented his own divisions of the tetrachord and the octave, which he derived with the help of a monochord. Ptolemy's astronomical interests also appeared in a discussion of the "music of the spheres."
Other works
His Optics, a work which survives only in a poor Arabic translation and in about twenty manuscripts of a Latin translation of the Arabic, made by Eugene of Palermo (circa 1154). In it he writes about properties of light, including reflection, refraction, and color. The work is a significant part of the early history of optics.
Ptolemaeus lunar crater

Ptolemaeus
from Apollo 16. NASA photo.
Coordinates 9.2° S, 1.8° W
Diameter 153 km
Depth 2.4 km
Colongitude 3° at sunrise
Eponym Claudius Ptolemaeus
Ptolemaeus is an ancient lunar impact crater close to the center of the near side. To the south-southeast Ptolemaeus is joined to the rim of Alphonsus crater by a section of rugged, irregular terrain, and these form a prominent chain with Arzachel to the south. To the southeast is Albategnius crater and to the north is the smaller but well-defined Herschel crater.
The features of Ptolemaeus are highlighted when the sun is at low angles during the first and last quarter. During the full moon the sun is directly overhead and the crater contours become more difficult to discern.
The crater has a low, irregular outer rim that is heavily worn and impacted with multiple smaller craters. The rim has a discernible polygonal shape, although overall it remains circular. The largest of the peaks along the rim, designated Ptolemaeus Gamma (?), has an altitude of 2.9 km and is located along the northwest rim. The crater has no central peak, a lava-flooded floor, and lacks a ray system. Impact sites of this form are often classified as a "walled-plain", due to their resemblance to the maria.
The somewhat dark-hued floor of Ptolemaeus is notable for several "ghost" craters, formed when lava flow covers a pre-existing crater. These leave only a slight rise where the rim existed, and are difficult to detect except at low angles of sunlight. There are also multiple smaller craters across the floor surface, most notably Ammonius crater in the northeastern quadrant.
On either of this crater are linear, irregular gashes in the lunar surface, forming valley-like features. These features are approximately parallel to each other and radiate from the direction of Mare Imbrium to the north-northwest.

L'École d'Athènes de Raphaël, montrant Zoroastre et Ptolémée.
Claudius Ptolemaeus, communément appelé Ptolémée (Ptolémaïs de Thébaïde (Haute-Égypte) vers 90 - Canope vers 168) était un astronome et astrologue grec qui vécut à Alexandrie (aujourd’hui en Égypte). Il est également l’un des précurseurs de la géographie.
Ptolémée fut l’auteur de plusieurs traités scientifiques, dont deux ont exercé par la suite une très grande influence sur les sciences islamique et européenne. L’un est le traité d’astronomie, qui est aujourd’hui connu sous le nom de l’Almageste (Le grand traité). L’autre est la Géographie, qui est une discussion approfondie sur les connaissances géographiques du monde gréco-romain.
L’astéroïde (4001) Ptolémée (4001 Ptolemaeus) a été nommé en son honneur, tout comme les cratères Ptolémée sur Mars et sur la Lune et aussi une tempête sur Vénus.
Astronomie
Ptolémée est l’auteur d’un traité d’astronomie connu sous le nom de l’Almageste (Al en arabe, suivi d’un superlatif grec signifie « le très grand »). Dans ce travail, il a proposé un modèle géocentrique du système solaire, qui fut accepté dans les mondes occidental et arabe pendant plus de mille trois cents ans. Aussi, ce système a été reconnu en Europe et utilisé comme référence pendant plus de 14 siècles avant que Nicolas Copernic n'élabore sa théorie: le système héliocentrique ou héliocentrisme (1543), appuyé par Galileo Galilei (Galilée), qui fut accusé d'hérésie par l'Église. L’Almageste contient également un catalogue d’étoiles et une liste de quarante-huit constellations, antérieure au système moderne de constellations bien que ne couvrant pas toute la sphère céleste. Ptolémée a décrit l'astrolabe inventé probablement par Hipparque.
Géographie

La carte du monde de Ptolémée, reconstituée à partir de sa Géographie (vers 150), indique les pays de Serica, Sinae (Chine) à l’extrême droite, au-delà de l’île de Taprobane (Sri Lanka, trop grande) et l’Aurea Chersonesus (Asie du Sud-Est).
Sa Géographie est une autre œuvre majeure. Il s’agit d’une compilation des connaissances de la géographie du monde à l’époque de l’empire romain. Ptolémée s'est essentiellement appuyé sur les travaux d’un autre géographe, Marinus de Tyr, et sur les index géographiques des empires romain et perse, mais la plupart de ses sources au-delà du périmètre de l’empire étaient d’origines douteuses.
La première partie de la Géographie est une discussion sur les données et les méthodes qu’il a utilisées. Comme pour le modèle du système solaire dans l’Almageste, Ptolémée unifia dans un grand ensemble toutes les informations dont il disposait. Il attribua des coordonnées à tous les lieux et particularités géographiques qu’il connaissait, dans une grille qui couvrait le globe. La latitude était mesurée à partir de l’équateur, comme aujourd’hui, mais Ptolémée préférait l’exprimer selon la durée du jour le plus long plutôt qu’en degrés (la durée du solstice d’été passe de 12 h à 24 h au fur et à mesure qu’on s’éloigne de l’équateur vers le cercle polaire). Il fixa le méridien de longitude 0 au point le plus à l’ouest qu’il connaissait, les Canaries.
Ptolémée imaginait aussi
et fournissait des instructions sur la façon de dessiner des cartes, à la
fois de tout le monde habité (écoymène) et des provinces romaines.
Dans la deuxième partie de la Géographie, il fournissait les listes
topographiques nécessaires, et des légendes aux cartes. Son écoymène
couvrait 180 degrés de longitude des Canaries (dans l’océan Atlantique)
jusqu’à la Chine, et environ 80 degrés de latitude de l’Arctique aux
Indes et loin en Afrique. Ptolémée était bien conscient que ses
connaissances ne couvraient qu’un quart du globe.
Malheureusement, les plus vieilles cartes des manuscrits de la Géographie de
Ptolémée ne datent que de 1300 environ, après la redécouverte du texte par
Maximus Planudes.
Astrologie
Le traité de Ptolémée sur l’astrologie, le Tetrabiblos, était l’ouvrage astrologique le plus célèbre de l’Antiquité. Il exerça une grande influence dans l’étude des corps célestes dans la sphère sublunaire. Ainsi, il fournissait des explications des effets astrologiques des planètes, en fonction de leurs effets chauffant, rafraîchissant, mouillant, et séchant.
Musique
Ptolémée a également écrit les Harmoniques, un traité de musicologie de référence. Après une critique de approches de ses prédécesseurs, Ptolémée y plaide pour baser des intervalles musicaux sur des proportions mathématiques (contrairement aux partisans d'Aristoxène) soutenus par observation empirique (contrairement à l'approche purement théorique de l’École pythagoricienne). Il a présenté ses propres divisions du tétracorde et de l'octave, qu'il a dérivés avec l'aide d'un monocorde. L’intérêt de Ptolémée pour l’astronomie apparaît également dans une discussion sur la musique des sphères.
Mathématiques
Ptolémée a découvert un théorème qui dit que si un quadrilatère non croisé est inscrit dans un cercle alors le produit de ses diagonales est égal à la somme des produits de ses côtés opposés. Il a aussi découvert une façon de calculer pi en utilisant la base 60.